Олимпиадная задача по планиметрии для 9–11 классов от Мякишева А. Г. — пересечение отрезка XY в выпуклом четырехугольнике
Задача
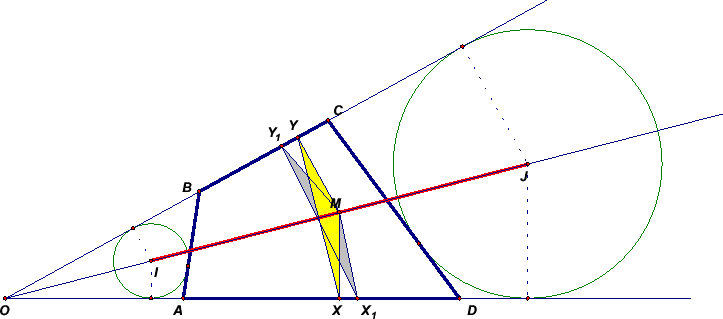
Дан выпуклый четырехугольник ABCD. Прямые BC и AD пересекаются в точке O, причём B лежит на отрезке O и A на отрезке OD. I – центр вписанной окружности треугольника OAB, J – центр вневписанной окружности треугольника OCD, касающейся стороны CD и продолжений двух других сторон. Перпендикуляры, опущенные из середины отрезка IJ на прямые BC и AD, пересекают соответствующие стороны четырёхугольника (не продолжения) в точках X и Y. Доказать, что отрезок XY делит периметр четырёхугольника ABCD пополам, причём из всех отрезков с этим свойством и концами на BC и AD XY имеет наименьшую длину.
Решение
Используя тот факт, что отрезки касательных, проведённые из одной точки, равны, несложно показать, что отрезок X'Y' с концами на сторонах AD и BC делит периметр пополам тогда и только тогда, когда OX' + OY' = l, где l – постоянная величина, равная удвоенному отрезку соответствующей касательной плюс полупериметр четырёхугольника.
Пусть M – середина IJ. Также просто проверяется, что OX + OY = l. Значит, треугольники MXX' и MYY' равны, а следовательно, треугольники MXY и MX'Y' подобны по двум углам. Значит, X'Y' минимально, когда минимально MX', то есть когда X' совпадает с X (см. рис.).
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь