Назад

Олимпиадная задача по планиметрии: хорда на MP и окружности с диаметром BC, 8-9 класс

Задача 203939 • Сложность: 3 • 8-9 класс
Задача

В треугольнике ABC угол A равен α,  BC = a.  Вписанная окружность касается прямых AB и AC в точках M и P.

Найти длину хорды, высекаемой на прямой MP окружностью с диаметром BC.

Авторы:
Шарыгин И. Ф.
Разделы:
Планиметрия
Источники:
I Олимпиада по геометрии имени И.Ф. Шарыгина (2005 г.) 11 класс Олимпиады и турниры Олимпиада по геометрии имени И.Ф. Шарыгина
Количество версий:
5
Решение

  Первый способ. Расстояние от центра окружности до указанной хорды равно полусумме расстояний от точек B и C до прямой MP, то есть

½ (BM sin∠AMP + CP sin∠APM) = ½ (BM + CP) cos α/2 = a/2 cos α/2  (рис. слева).

  Соответственно, длина хорды равна  a sin α/2.

             
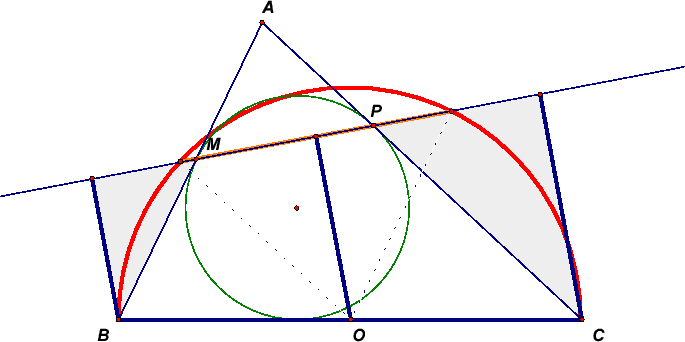
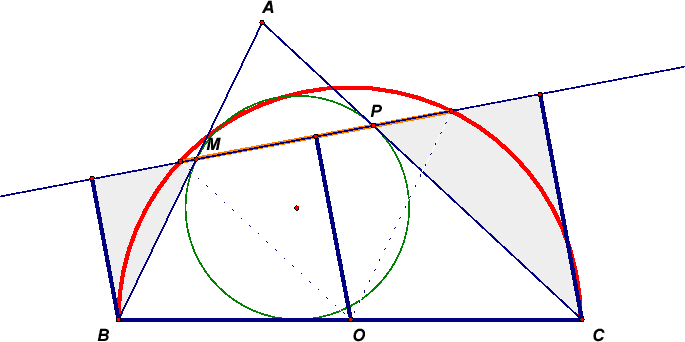
  Второй способ. Пусть I – центр вписанной окружности треугольника, X, Y – точки пересечения прямых BI, CI с прямой MP (рис. справа). Тогда

∠MXB = ∠AMP – ∠MBX = ½ ∠C.  Следовательно, треугольники BXM и BCI подобны, то есть  BX : BC = BM : BI.  Значит, треугольники BXC и BMI также подобны, то есть угол BXC – прямой. Аналогично угол BYC прямой. Следовательно, искомая хорда

XY = BC sin∠XCY = a sin α/2  (∠XCY = 90° – ½ ∠B – ½ ∠С = α/2).

Ответ

a sin α/2.

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет