Олимпиадная задача по планиметрии: Хулиганы Джей и Боб, площадь головастиков
Задача
Хулиганы Джей и Боб на уроке черчения нарисовали головастиков
(четыре окружности на рисунке - одного радиуса, треугольник - равносторонний,
горизонтальная сторона этого треугольника - диаметр окружности). Какой из
головастиков имеет бо'льшую площадь?
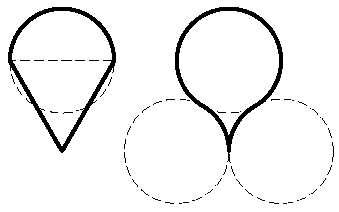
Решение
Ответ: площади фигур равны.Первое решение. Пусть площадь окружности равна Sокр, а площадь равностороннего треугольника со стороной, равной диаметру окружности, равна Sтр. Так как треугольник O1O2O3 равносторонний, его углы равны 60o, кроме того длина его стороны равна диаметрам исходных окружностей, поэтому его площадь равна Sтр.. Значит, площадь каждого из заштрихованных секторов на рис. 20 равна Sокр/6, а площадь закрашенной части равна
 |
 |
| Рис. 20 | Рис. 21 |
Поэтому площадь второго головастика равна Sокр+Sтр-(Sокр/2)=Sокр+(Sокр/2). Очевидно, это совпадает с площадью второго головастика. Идея второго решения. Наложим одного головастика на другого как показано на рис. 21. Нетрудно проверить, что если отрезать от первого головастика заштрихованные сегменты, и повернуть их вокруг точек A1 и B1 на 180o, то получится в точности второй головастик.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь