Олимпиадная задача по делимости и многочленам для 8–10 класса от Сендерова В. А.

  Предположим, что при некотором  a > 3  A = (a^m₁ – 1)...(a^m_n – 1) = (a^k₁+1)...(a^k_l + 1).

  Докажем сначала, что как любое m_i, так и число  a – 1  являются степенями двойки. Пусть γ – нечётный делитель числа m_i, а p – любой простой делитель числа  a^γ – 1.  Тогда в правом произведении найдётся множитель  a^k_j + 1,  кратный p. Поэтому число  (a^γk_j + 1) – (a^γk_j – 1) = 2  кратно p, то есть все простые делители числа  a^γ – 1  – двойки и  (a^γ–1 + ... + a + 1)(a – 1) = a^γ – 1 = 2^s.  Поскольку  a > 3,  то  s > 1  и γ нечётно, поэтому выражение в первой скобке – нечётный делитель числа 2^s. Значит, γ и  a – 1 = 2^s.  В частности,  a – 1  делится на 4, поэтому  a^k + 1 ≡ 2 (mod 4).

  Каждое число в левой части исходного равенства представляется в виде  a^2d – 1 = (a – 1)(a + 1)(a² + 1)(a⁴ + 1)...(a^2d–1 + 1) = 2^s·2^da₀...a_d–1 , где

a_i = ½ (a²ⁱ + 1)  – нечётные числа. Заметим, что при  m > n  число  a^2m – 1  делится на  a²ⁿ + 1,  поэтому  НОД(a_m, a_n) ≤ (a^2m + 1) – (a^2m – 1) = 2;  поскольку a_i нечётны, они попарно взаимно просты. Пусть q – максимальная степень двойки, входящая в m_i или k_j. Тогда 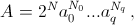    причём

N > N₀ + ... + N_q,  так как это справедливо для любого представления  a^2d – 1.

  Ни один из множителей  a^k_j + 1  не делится на 4, поэтому их в представлении числа A не меньше N. Но каждое из них делится на одно из чисел a_i: если  k_j = 2^rb,  где b нечётно, то  a^k_j + 1  делится на a_r. Поскольку  N > N₀ + ... + N_q,  то на какое-то число a_i делится больше, чем N_i чисел  a^k_j + 1,  а следовательно, A делится на большую степень a_i, чем N_i. Противоречие с тем, что a_i нечётны и попарно взаимно просты.

2 и 3.