Олимпиадная задача по планиметрии: треугольник, прямоугольники и точка пересечения

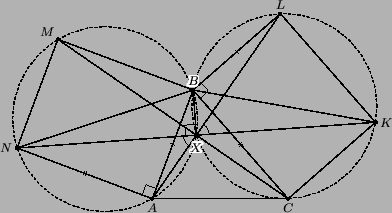
Решение 1:Рассмотрим окружности, описанные около данных прямоугольников. Обозначим вторую точку их пересечения через X. Тогда  ∠BXN = ∠BXK = 90°.  Значит, точки N, X, K лежат на одной прямой, перпендикулярной BX. Кроме того, треугольники NAB и KLB равны. Поэтому

∠NXA = ∠NBA = ∠LBK = ∠LXK,  а значит, точки A, X, L также лежат на одной прямой. Аналогично, точки M, C, X лежат на одной прямой. Итак, X – точка пересечения этих трёх прямых.

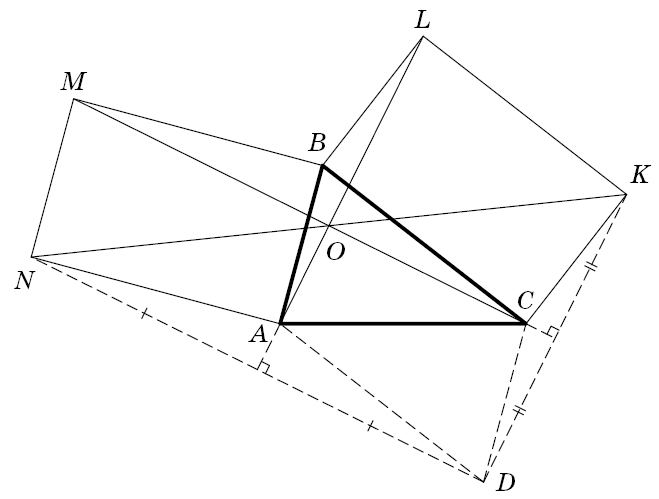
Решение 2:Достроим исходный треугольник до параллелограмма ABCD.

ТогдаALKDиCDNMтакже параллелограммы. Равнобедренный треугольникCBMполучается из треугольникаLBAповоротом на 90°, поэтому  CM⊥AL || KD.  Значит, прямаяCM– серединный перпендикуляр к отрезкуKD. АналогичноAL– серединный перпендикуляр кND. Следовательно, прямыеCMиAL– средние линии прямоугольного треугольникаKDNи проходят через середину его гипотенузыKN.

Решение 3:Пусть F и G – середины отрезков AL и CM соответственно, X – точка пересечения этих отрезков. Тогда BFXG – прямоугольник (угол CBM получается из угла ABL поворотом на 90°, значит, и биссектрисы этих углов перпендикулярны).

то естьX– середина отрезкаKN.

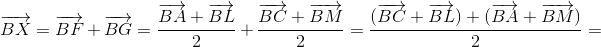
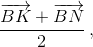
Ответ задачи отсутствует