Олимпиадная задача по стереометрии о пересечении 8 многогранников с вершиной A (уровень 10–11 класс)

  Сделаем гомотетию исходного многогранникаMс центром в точкеAи коэффициентом 2. Объем растянутого многогранникаM'будет в 8 раз больше объема многогранникаM. Докажем, что все 8 "перенесенных" многогранников содержатся вM'. Пусть вершину A перенесли в вершину B, X — произвольная точка многогранника M, Y — образ точки X при соответствующем параллельном переносе (рис.). Докажем, что точка Y принадлежит M'.

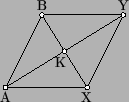
Отрезок BX целиком содержится в многограннике M, так как многогранник — выпуклый. Значит, его середина K принадлежит многограннику. Четырехугольник ABYX — параллелограмм, поэтому Y получается из K гомотетией с центром в точке A и коэффициентом 2, следовательно, точка Y принадлежит M'.

Заметим, что точки вблизи вершины A не принадлежат ни одному из "перенесенных" многогранников. Действительно, расположим многогранник так, чтобы вершина A была выше всех остальных вершин, тогда существует плоскость, которая проходит ниже вершины A, но выше всех остальных вершин. Эта плоскость отрезает от многогранника M маленький многогранник N, содержащий точку A. Ясно, что он не пересекается ни с одним из перенесенных многогранников.

Предположим теперь, что перенесенные многогранники не пересекаются по внутренним точкам, тогда объем многогранника M' не меньше, чем сумма объема многогранника N и объемов перенесенных многогранников. Но суммарный объем перенесенных многогранников в точности равен объему многогранника M'. Противоречие.

Комментарии. 1^o. Задача легко обобщается для n-мерного пространства.

2^o. Более слабая формулировка задачи была на XIII Международной математической олимпиаде. Требовалось доказать, что пересекаются хотя бы два из девяти (а не восьми) многогранников.

Ответ задачи отсутствует