Олимпиадная задача Ковальджи В. К. о стоимости перевозки по комбинаторике для 8-10 классов
Задача
Несколько населённых пунктов соединены дорогами с городом, а между ними дорог нет. Автомобиль отправляется из города с грузами сразу для всех населённых пунктов. Стоимость каждой поездки равна произведению веса всех грузов в кузове на расстояние. Докажите, что если вес каждого груза численно равен расстоянию от города до пункта назначения, то общая стоимость перевозки не зависит от порядка, в котором объезжаются пункты.
Решение
Решение 1: Докажем сначала, что от перестановки порядка двух последовательных поездок стоимость перевозки не изменится. Пусть автомобиль посетил некоторый населённый пункт M, а потом – населённый пункт N, причём расстояния до M и N равны m и n соответственно. Тогда веса соответствующих грузов – тоже m и n. Стоимость перевозки остальных грузов не меняется от перестановки поездок в M и N. Стоимость перевозок грузов m и n в города, отличные от M и N, тоже не изменится. Стоимость перевозки грузов m и n в города M и N равна (m + n)m + n(m + n), а после перестановки – (m + n)n + m(n + m). Обе стоимости равны (m + n)².
Пусть есть два разных порядка объезда населённых пунктов. Первый порядок можно превратить во второй, переставляя последовательные поездки (это известно из теории перестановок). При каждой такой перестановке общая стоимость перевозки не меняется, значит, она не зависит от порядка объезда населённых пунктов.
Решение 2: Занумеруем грузы a1, a2, ..., an в том порядке, в каком их развозят. Тогда стоимость перевозки равна
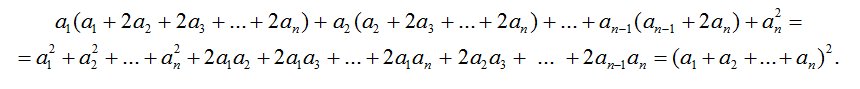
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь