Назад

Олимпиадная задача: Суммы пар и квадраты для n=9, 11, 1996 (8-10 класс)

Задача 207806 • Сложность: 3 • 8-10 класс
Задача

Целые числа от 1 до n записаны в строчку. Под ними записаны те же числа в другом порядке. Может ли случиться так, что сумма каждого числа и записанного под ним есть точный квадрат  а) при  n = 9,   б) при  n = 11,   в) при  n = 1996.

Решение

  а) Например:

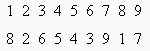
  б) Нетрудно видеть, что под числом 11 может быть записано только число 5, но под числом 4 тоже может быть записано только число 5. Противоречие.   в) Запишем под числом k число  2025 – k  для всех  k = 29, 30, ..., 1996.  Тогда сумма чисел в каждом столбце, начиная с 29-го, равна 45², а числа от 1 до 28 остались "неиспользованными".

  Далее под числами  k = 21, 22, ..., 28  запишем числа  49 – k.  Затем под числами  k = 16, 17, 18, 19, 20 запишем числа  36 – k.  Наконец, каждому  k = 1, 2, ..., 15  поставим в соответствие число  16 – k.

Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет