Олимпиадная задача по планиметрии и комбинаторной геометрии для 9–11 класса: покрытие круга полосами

Решение 1:   Пусть суммарная ширина полос не меньше 2,5π.

  Будем считать, что горизонтальных и вертикальных полос нет. Упорядочим полосы по возрастанию угла наклона относительно положительной полуоси Ox, а полосы с одинаковым углом наклона сложим в одну полосу. Можно считать, что суммарная ширина полос с углом наклона, меньшим 90°, не меньше ^5π/₄ (иначе отразим плоскость относительно оси Oy).

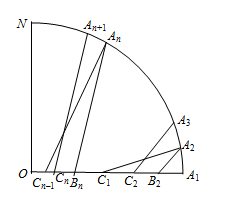
  Рассмотрим дугу A₁N длины ^5π/₄, отсекаемую первой четвертью от окружности радиуса 2,5 с центром в точке O (начале координат) (см. рис.). Пусть m таково, что   d₁ + d₂ + ... + d_m–1 < ^5π/₄,   d₁ + d₂ + ... + d_m ≥ ^5π/₄.

  Разделим дугуA₁Nна части точками  A₂, ...,A_m  так, что длина дугиA_nA_n+1равнаd_n. Перенесёмn-ю полосу так, чтобы её нижний край прошёл через точкуA_n. Пусть этот нижний край пересекает ось абсцисс в точкеB_n. Эта полоса, очевидно, содержит точкуA_n+1, а значит, покрывает криволинейную трапециюB_nA_nA_n+1C_n(точкаC_nтакже лежит на оси абсцисс).   Докажем по индукции, что для каждого  n < m  первыеnполос покрывают криволинейный треугольникA₁A_n+1C_n(см. рис.).   При  n= 1  утверждение очевидно.  Шаг индукции. По предположению индукции первые  n– 1  полосок покрывают криволинейный треугольникA₁A_nC_n–1и, тем более, криволинейный треугольникA₁A_nB_n(поскольку точкаB_nлежитправееточкиC_n–1). Добавив к нему "трапецию"B_nA_nA_n+1C_n, покрытуюn-й полоской, мы и получим криволинейный треугольникA₁A_n+1C_n.   Добавивm-ю полоску, мы покроем секторOA₁N. 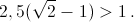Легко видеть, что радиус вписанного в этот сектор (и следовательно, покрытого полосками) круга равен     Замечание. Суммарную ширину полосок можно уменьшить до 2π. Пусть суммарная ширина полосок с углом наклона, не превышающим ^π/₂, равна  α ≥ π,  а суммарная ширина остальных полосок равна  2π – α.  Рассмотрим полукруг радиуса 2, лежащий в верхней полуплоскости (см. рисунок).   Рассуждая как выше, покроем полосками первого типа криволинейный треугольникAKC, где длина дугиAKравна α. Аналогично полосками второго типа (начав с точкиD) покроем криволинейный треугольникDKE, где длина дугиDKравна  2π – α.  Тем самым будет покрыт весь полукруг радиуса 2, а в него можно вписать круг радиуса 1.

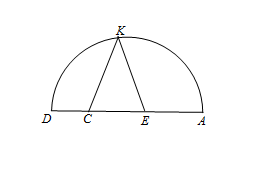
Решение 2:   Будем считать, что сумма ширин полос не меньше 24. Каждой полосе поставим в соответствие вектор, перпендикулярный её границе, длина которого равна ширине этой полосы. Отложим их от одной и той же точки O.

  Разобьём плоскость на 12 углов величины 30° с вершиной в точке O. Для каждого из углов подсчитаем сумму длин векторов, лежащих внутри или на границе этого угла или внутри или на границе вертикального ему угла. Получим шесть величин – по одной для каждой пары вертикальных углов.

   Выберем ту пару вертикальных углов, для которой подсчитанная сумма оказалась  24 : 6 = 4  (такая, очевидно, найдётся). Заменив, если потребуется, некоторые векторы на противоположные, добьёмся того, чтобы все они попали в один и тот же угол величины 30°.

  Сумма векторов не зависит от порядка, в котором берутся слагаемые. Упорядочим векторы так, чтобы направление следующего получалось из направления предыдущего поворотом по часовой стрелке. Отложим их, прикладывая начало каждого следующего вектора к концу предыдущего. Получим выпуклую ломаную OO₁O₂...O_n (см. рисунок). Длина этой ломаной не меньше 4.

  Длина отрезка OO_n не меньше чем 2. Действительно, угол между отрезком OO_n и любым из отрезков ломаной не больше 30°, значит, длина проекции отрезка O_iO_i+1 на прямую OO_n не меньше, чем  O_iO_i+1·cos 30°.  Суммируя по всем отрезкам ломаной, получаем требуемое неравенство.

  Перенесём полоски параллельно так, чтобы концы каждого из отрезков  OO₁, O₁O₂, ..., O_n–1O_n  лежали на границе соответствующих полосок. Докажем, что многоугольник MOO₁O₂...O_n, где точка M – пересечение перпендикуляров к отрезкам OO₁ и O_n–1O_n, проведённых к этим отрезкам в точках O и O_n, будет полностью покрыт полосками.

  Для этого рассмотрим любую точку X, лежащую в многоугольнике MOO₁O₂...O_n. Проще всего рассмотреть ближайшую к X точку Y на ломаной OO₁O₂...O_n. Если Y лежит на O_iO_i+1, то  XY ⊥ O_iO_i+1,  так что точка X покрывается полоской, перпендикулярной отрезку O_iO_i+1.

Ответ задачи отсутствует