Олимпиадная задача по планиметрии: биссектрисы треугольника и равные отрезки (8-9 класс)
Задача
AK – биссектриса треугольника ABC, P и Q – точки на двух других биссектрисах (или на их продолжениях) такие, что PA = PK и QA = QK.
Докажите, что ∠PAQ = 90° – ½ ∠A.
Решение
Пусть точка P лежит на биссектрисе угла B, а точка Q – на биссектрисе угла C. По условию точка P лежит на серединном перпендикуляре l к отрезку AK. Прямая l имеет с прямой, на которой лежит биссектриса угла B, ровно одну общую точку, так как в противном случае две биссектрисы треугольника были бы параллельными или перпендикулярными, что невозможно (сумма двух углов треугольника меньше 180°). Таким образом, точка P определена однозначно.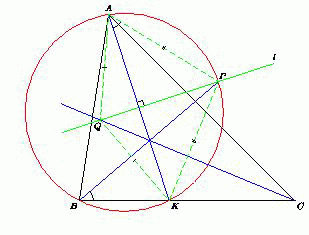 
Опишем окружность вокруг треугольника ABK. Пусть луч BP вторично пересекает эту окружность в середине дуги AK. Эта середина также лежит на серединном перпендикуляре l и, следовательно, совпадает с точкой P. Значит, ∠KAP = ∠PBK = ½ ∠B. Аналогично ∠KAQ = ½ ∠C.
Таким образом, ∠PAQ = ∠KAP + ∠KAQ = ½ (∠B + ∠C) = 90° – ½ ∠A.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь