Олимпиадная задача по планиметрии для 8-9 классов от Шарыгина: Расстояние между ортоцентрами в треугольнике
Задача
Сторона AB треугольника ABC равна c. На стороне AB взята такая точка M, что ∠CMA = φ.
Найдите расстояние между ортоцентрами треугольников AMC и BMC.
Решение
Пусть Da и Db – проекции ортоцентров Ha и Hb треугольников AMC и BMC на прямую CM (см. рис.). 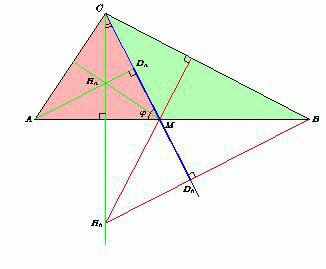 Точки Ha и Hb лежат лежат на перпендикуляре, опущенном из C на прямую AB. Отрезок DaDb – проекция отрезка AB на прямую CM, а так как угол между прямыми AB и CM равен φ или 180° – φ,  то DaDb = AB |cos φ| = c |cos φ|.
Точки Ha и Hb лежат лежат на перпендикуляре, опущенном из C на прямую AB. Отрезок DaDb – проекция отрезка AB на прямую CM, а так как угол между прямыми AB и CM равен φ или 180° – φ,  то DaDb = AB |cos φ| = c |cos φ|.
С другой стороны, отрезок DaDb – проекция отрезка HaHb на прямую CM, а так как угол между прямыми HaHb и CM равен 90° – φ или 90° + φ, то 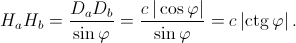
Ответ
c |ctg φ|.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет