Олимпиадная задача по планиметрии: перпендикулярность прямых в треугольнике ABC
Задача
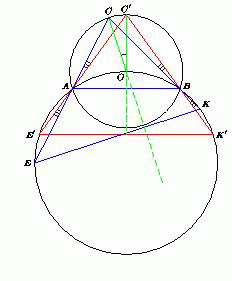
Треугольник ABC вписан в окружность с центром O. Прямые AC и BC вторично пересекают окружность, проходящую через точки A, O и B, в точках E и K. Докажите, что прямые OC и EK перпендикулярны.
Решение
Утверждение очевидно в случае, когда точка C совпадает с серединой C' дуги ACB. Пусть ∠COC' = α. Тогда угол между прямыми E'K' и EK равен ∠EAE' + ∠KBK' = ∠CAC' + ∠CBC' = α. Значит, прямые EK и OC получаются из прямых E'K' и OC' поворотом на угол α, а так как OC' ⊥ E'K', то
OC ⊥ EK.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет