Олимпиадная задача по планиметрии: геометрическое место точек в равностороннем треугольнике для классов 8–9
Задача
Дан равносторонний треугольник ABC. Для произвольной точки P внутри треугольника рассмотрим точки A' и C' пересечения прямых AP с BC и CP с AB. Найдите геометрическое место точек P, для которых отрезки AA' и CC' равны.
Решение
Выберем произвольную точку A' внутри стороны BC и проведём отрезок AA'. Очевидно, что среди отрезков с началом в точке C и концом на стороне AB имеются только два, равных отрезку AA'. Это такие отрезки CC1 и CC2, что ∠C1CA = ∠C2CB = ∠A'AC (см. рис.).
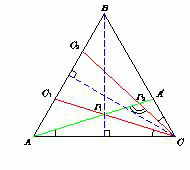
Ответ
Фигура, состоящая из высоты BH (без точек B и H) и дуги AOC (без точек A и C).
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет