Олимпиадная задача по планиметрии: угол проекции вписанной окружности на гипотенузу

  Пусть O – центр, а r – радиус вписанной окружности прямоугольного треугольника ABC, P, Q и T – точки касания этой окружности соответственно с катетами AC, BC и гипотенузой AB; MN – проекция окружности на гипотенузу (см. рис.).   Первый способ. Поскольку CPOQ – квадрат со стороной r, то  OC = r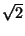.  Аналогично находим, что  OM = ON = r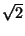.  Значит, точки C, M и N лежат на окружности с центром O и радиусом r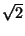.  Поскольку MON – центральный угол этой окружности, а MCN – вписанный, то  ∠MCN = ½ ∠MON = 45°.  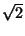 Второй способ. Через точки M и N проведём касательные к окружности, не совпадающие с прямой AB (см. рис.). Пусть X и Y – точки их касания с окружностью, а F и G – точки их пересечения с катетами AC и BC соответственно. Тогда  CF = CP+ PF = r + PF = r + FX = MX + FX = MF.

  Значит, треугольник CFM – равнобедренный. Аналогично треугольник CNG – равнобедренный. Проведём высоту CH треугольника ABC. Тогда

MF || CH || NG,  поэтому  ∠HCM = ∠CMF = ∠MCF,  ∠HCN = ∠CNG = ∠NCG.  Следовательно,  ∠MCN = ∠HCM + ∠HCN = ½ ∠C = 45°.

45°.