Олимпиадная задача по планиметрии: угол BPC в треугольнике ABC, 8-9 класс

Решение 1:Пусть Q – точка пересечения отрезка CP с высотой BH данного равнобедренного треугольника, опущенной на основание.

Тогда  ∠QAC= ∠ACQ= 30°,  ∠BAQ= 20°,  ∠BAP= 10° = ½ ∠BAQ.  Значит,AP– биссектриса углаBAQ. По теореме о внешнем угле треугольника ∠AQP= ∠ACQ+ ∠CAQ= 60°,  ∠AQB= ∠QAC+ ∠AHQ= 120°.  ПоэтомуQP– биссектриса углаAQB. Таким образом,P– точка пересечения биссектрис треугольникаABQ. Следовательно,  ∠BPC= ∠BPQ= 90° + ½ ∠BAQ= 90° + 10° = 100°.

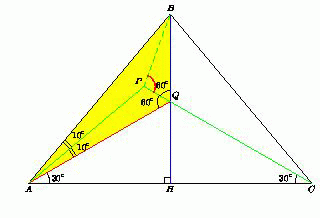
Решение 2:Построим равносторонний треугольник ABD (см. рис.). Тогда  BD = BC,  то есть треугольник CBD – равнобедренный и

∠BDC = ∠BCD = (180° – 80° – 60°) : 2 = 20°.  Значит, точка P лежит на отрезке CD.

∠PAD= 70°,  ∠ADP= 40°,  поэтому  ∠DPA= 70°,  и треугольникADP– равнобедренный. Значит, треугольникBDP– тоже равнобедренный, ∠BPD= (180° – 20°) : 2 = 80°,  а  ∠BPC= 100°.

100°.