Олимпиадная задача Шарыгина: планиметрия для 8–9 класса о вписанной окружности

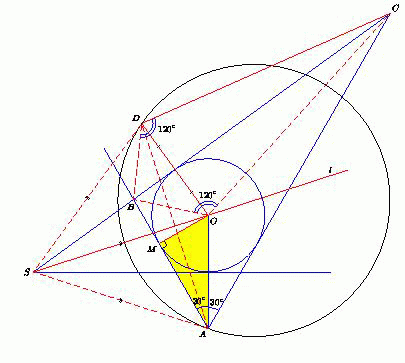
  Пусть r – радиус окружности, вписанной в данный угол с вершиной S, M – точка касания этой окружности с прямой AB. Поскольку точка A симметрична точке O относительно стороны данного угла, то  OA = 2r.  Из прямоугольного треугольника OAM находим, что  OM : OA = r : 2r = 1 : 2.  Значит,  ∠OAM = 30°,  ∠BAC = 2∠OAM = 60°.

  Поскольку BO и CO биссектрисы углов ABC и ACB треугольника ABC, то  ∠BOC = 90° + ½ ∠BAC = 120°.

  ПустьD– точка, симметричная точкеOотносительно прямойBC. Тогда  ∠BDC= ∠BOC= 120° = 180° – ∠BAC.  Поэтому около четырёхугольникаABDCможно описать окружность. Центр этой окружности лежит на серединном перпендикуляреlк хордеAD, а так как  SD = SO = SA  и ∠DSO= ∠ASO  (в силу симметрии), то треугольникASD– равнобедренный, аSO– биссектриса его угла при вершине. Следовательно, биссектриса данного в условии угла лежит на прямойl. Таким образом, центр описанной окружности четырёхугольникаABDC(а значит, и треугольникаABC) лежит на этой биссектрисе.

Ответ задачи отсутствует