Олимпиадная задача по планиметрии: деление угла BAD параллелограмма лучами AM и AN
Задача
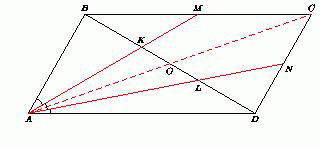
В параллелограмме ABCD точки M и N – середины сторон BC и CD соответственно. Могут ли лучи AM и AN делить угол BAD на три равные части?
Решение
Предположим, что это возможно. Пусть ∠BAM = ∠MAN = ∠DAN, лучи AM и AN пересекают диагональ BD в точках K и L соответственно, а O – центр параллелограмма. Поскольку K – точка пересечения медиан треугольника ABC, то BK = ⅔ BO = ⅓ BD.
Аналогично DL = ⅓ BD. Значит, BK = KL = DL. В треугольнике ABL медиана AK является биссектрисой, поэтому треугольник ABL – равнобедренный, а AK – его высота. Аналогично AL – высота треугольника AKD. Таким образом, AK ⊥ BD и AL ⊥ BD, то есть из точки A на прямую BD опущено два различных перпендикуляра, что невозможно.
Ответ
Не могут.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь