Олимпиадная задача по планиметрии: найти углы в треугольнике ABC, 8–9 класс

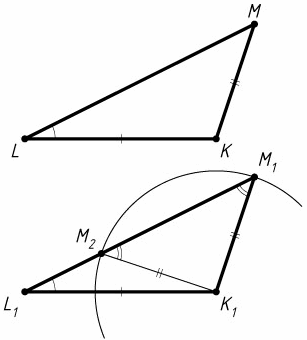
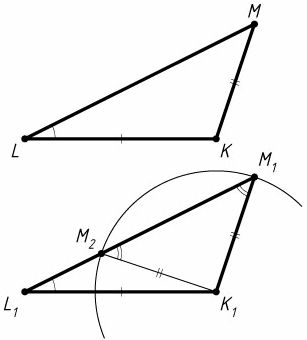
  Лемма. Если стороны K₁L₁, K₁M₁ и угол K₁L₁M₁ треугольника K₁L₁M₁ соответственно равны сторонам KL, KM и углу KLM треугольника KLM, то либо  ∠K₁M₁L₁ = ∠KML  и тогда треугольник K₁L₁M₁ равен треугольнику KLM, либо  ∠K₁M₁L₁ = 180° – ∠KML.

  Доказательство. Пусть дан треугольник KLM (см. рис.). Построим треугольник K₁L₁M₁ по данным сторонам K₁L₁ = KL,  K₁M₁ = K₁L₁  и углу K₁L₁M₁, равному углу KLM. Для этого от начала произвольного луча отложим отрезок L₁K₁ = LK,  затем в одну из плоскостей, на которые разбивает плоскость прямая L₁K₁, отложим луч L₁P, образующий с лучом L₁K₁ угол, равный данному углу KML. С центром в точке K₁ построим окружность радиусом, равным KM. Если эта окружность не пересекается с построенным лучом, то задача не имеет решений; если окружность имеет с лучом единственную общую точку, то задача имеет одно решение; если окружность пересекает луч в двух точках M₁ и M₂ (точка M₂ лежит L₁ и M₁), то треугольник M₁K₁M₂ – равнобедренный, поэтому  ∠K₁M₂L₁ = ∠K₁M₂M₁ = ∠K₁M₁M₂ = 180° – ∠K₁M₁L₁.

  Вернёмся к нашей задаче. Обозначим  ∠ABX = ∠YAC = α,  ∠AYB = ∠BXC = β (см. рис.).   ПосколькуAYBиBXC– внешние углы треугольниковAYCиAXB, то  ∠C= ∠ACY= ∠AYB– ∠YAC= β – α = ∠BXC–ABX= ∠BAX= ∠A.   Значит, треугольникABC– равнобедренный,  AB = BC.  Рассмотрим треугольникиXBCиYAB. Известно, что  BC = AB,  CX = YB  и  BXC= ∠AYB.  Из леммы следует, что либо треугольникиXBCиYABравны, либо  ∠XBC+ ∠YAB= 180°.  Второй вариант невозможен, так как в этом случае сумма углов треугольникаAYBбыла бы больше 180°. Из равенства треугольниковXBCиYABследует равенство угловCиB, значит, треугольникABC– равносторонний.

60°, 60°, 60°.