Назад

Олимпиадная задача по планиметрии и стереометрии для 8-9 класса: периметр треугольника MBN

Задача 208136 • Сложность: 3 • 8-9 класс
Задача

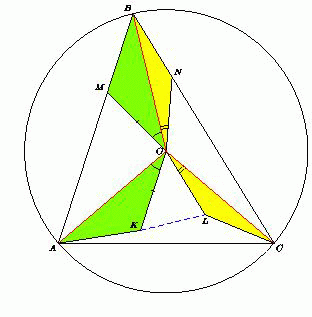
Пусть O – центр описанной окружности треугольника ABC. На сторонах AB и BC выбраны точки M и N соответственно, причём  2∠MON = ∠AOC.  Докажите, что периметр треугольника MBN не меньше стороны AC.

Решение
  Рассмотрим случай, изображённый на рисунке. При повороте вокруг точкиO, переводящем вершинуBвA, точкаMпереходит в некоторую точкуK, а при повороте вокруг точкиO, переводящем вершинуBвC, точкаNпереходит в некоторую точкуL. При этом треугольникAOKравен треугольникуBOM, а треугольникCOL– треугольникуBON. Поскольку  OK = OM,  OL = ON  и  ∠KOL=AOC– (∠AOK+ ∠LOC) = ∠AOC– ∠MON= ∠MON,  то треугольникиKOLиMONравны. Поэтому  KL = MN.  Следовательно,  PMBN = BM + MN + NB = AK + KL + LC ≥ AC.   Остальные случаи рассматриваются аналогично.
Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет