Олимпиадная задача по планиметрии: радиус описанной окружности треугольника BMK
Задача
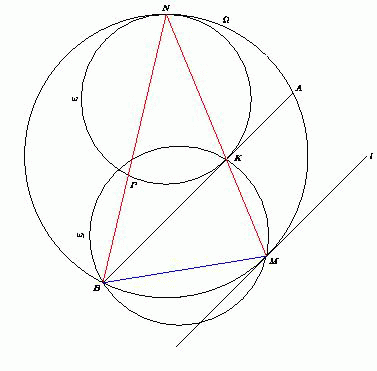
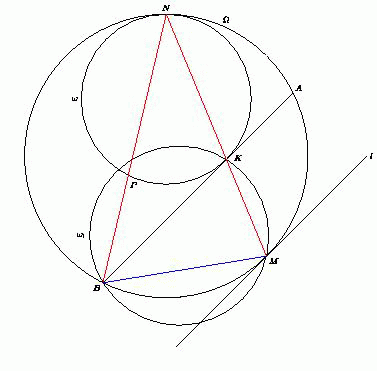
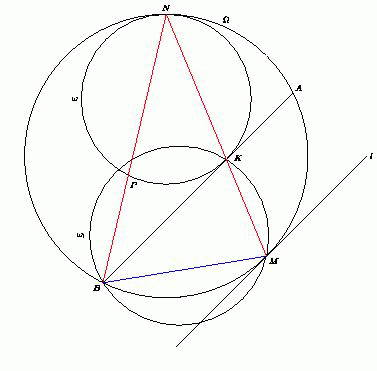
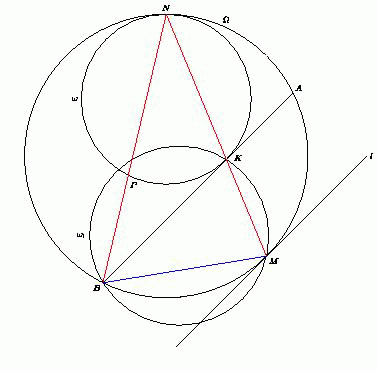
Даны две окружности, касающиеся внутренним образом в точке N . Касательная к внутренней окружности, проведённая в точке K , пересекает внешнюю окружность в точках A и B . Пусть M – середина дуги AB , не содержащей точку N . Докажите, что радиус окружности, описанной около треугольника BMK , не зависит от выбора точки K на внутренней окружности.
Решение

При гомотетии с центром в точке N и коэффициентом 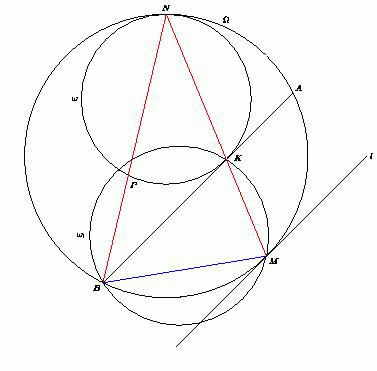 окружностьпереходит в окружность. Точка P при этом переходит в
точку B , а касательная AB к окружности, проведённая в точке K , –
в касательную l к окружности, параллелельную AB . Поскольку касательная l параллельна хорде AB , то точка касания – середина дуги AB ,
не содержащей точку N , т.е. точка M . Значит, точки N , K и M лежат на
одной прямой.
окружностьпереходит в окружность. Точка P при этом переходит в
точку B , а касательная AB к окружности, проведённая в точке K , –
в касательную l к окружности, параллелельную AB . Поскольку касательная l параллельна хорде AB , то точка касания – середина дуги AB ,
не содержащей точку N , т.е. точка M . Значит, точки N , K и M лежат на
одной прямой.
Пусть 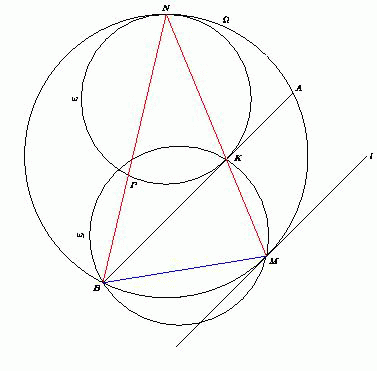 BMN = α . Из теоремы синусов следует, что
BMN = α . Из теоремы синусов следует, что
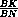 =
=  =
=  .
.
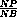 =
=  . По теореме о касательной и секущей BK2 = BP· BN . Значит,
. По теореме о касательной и секущей BK2 = BP· BN . Значит,
 )2 = (
)2 = (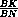 )2=
)2=
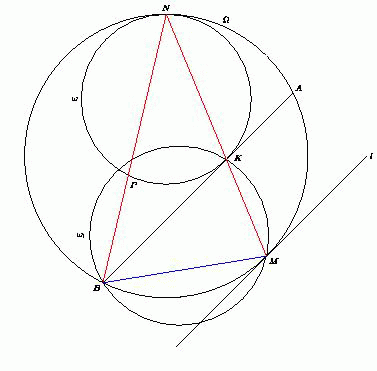 =
= =
=
 =
=  = 1-
= 1-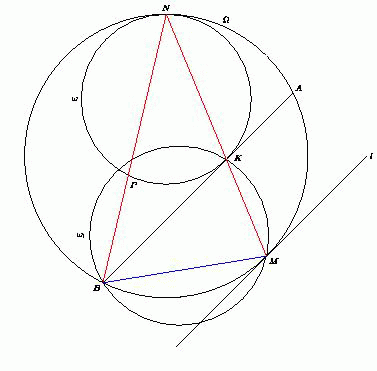 = 1-
= 1- .
.
 не зависит от выбора точки K , а значит,
и r1не зависит от выбора точки K .
не зависит от выбора точки K , а значит,
и r1не зависит от выбора точки K .
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь