Олимпиадная задача по планиметрии: теорема о прямоугольном треугольнике ABC (8–9 класс)
Задача
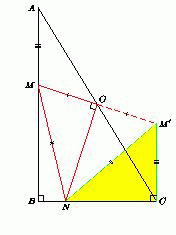
В прямоугольном треугольнике ABC точка O – середина гипотенузы AC . На отрезке AB взята точка M , а на отрезке BC – точка N , причём угол MON – прямой. Докажите, что AM2+CN2 = MN2.
Решение
При симметрии относительно точки O вершина A переходит
в вершину C , точка M – в некоторую точку M' , отрезок AM – в отрезок CM' , равный AM . При
этом, поскольку AM 
BC и CM'|| AM , то 
M'CN = 90o . Кроме того, в треугольнике MNM' высота NO является медианой, значит, M'N=MN .
Следовательно,
AM2+CN2 = CM'2+CN2 = M'N2 = MN2.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет