Олимпиадная задача по планиметрии: равноудалённость точки на стороне параллелограмма для 8-9 классов
Задача
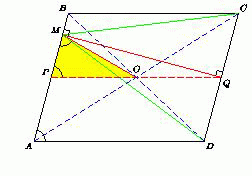
Диагонали параллелограмма ABCD пересекаются в точке O. Точка M лежит на прямой AB, причём ∠AMO = ∠MAD.
Докажите, что точка M равноудалена от точек C и D.
Решение
Пусть P и Q – середины сторон соответственно AB и CD. Тогда PQ || AD, а O – середина PQ. Предположим, что точка M не лежит на отрезке AP. Тогда ∠MPO = ∠MAD = ∠AMO. Поэтому треугольник MO = PO, то есть в треугольнике PMQ медиана MO равна половине стороны PQ. Значит,
MQ ⊥ MP || CD, то есть MQ – серединный перпендикуляр к отрезку CD. Следовательно, точка M равноудалена от точек C и D.
Аналогично разбирается случай, когда точка M лежит на отрезке AP.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет