Олимпиадная задача по планиметрии: точка пересечения диагоналей прямоугольника на прямой MN
Задача
Окружности S1 и S2 пересекаются в точках M и N. Докажите, что если вершины A и C некоторого прямоугольника ABCD лежат на окружности S1, а вершины B и D – на окружности S2, то точка пересечения диагоналей прямоугольника лежит на прямой MN.
Решение
Пусть O – точка пересечения диагоналей прямоугольника ABCD, а прямая MO вторично пересекает окружность S1 в точке N1, а окружность S2
– в точке N2. Поскольку точка O лежит внутри каждой окружности, то точки N1 и N2 лежат по одну сторону от O. По теореме о произведениях отрезков пересекающихся хорд
MO·ON1 = AO·OC = BO·OD = MO·ON2, поэтому ON1 = ON2. Значит, точки N1, N2 и N совпадают, а точка O лежит на отрезке MN. 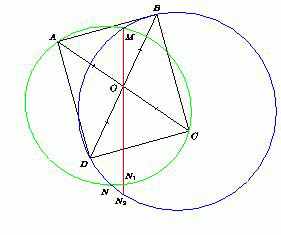
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет