Олимпиадная задача по планиметрии для 9-10 классов: описание окружностей и подобие треугольников

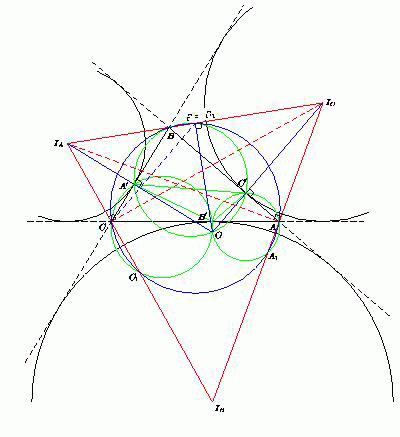
  Пусть I_A, I_B и I_C – центры вневписанных окружностей треугольника ABC, касающихся сторон BC, AC и AB соответственно. Точки I_A, I_С и B лежат на одной прямой – биссектрисе внешнего угла при вершине B треугольника ABC. Аналогично точки A и B лежат на отрезках I_CI_B и I_AI_B соответственно.

  Обозначим черезOточку пересечения продолжений радиусовI_AA'иI_CC'. В прямоугольных треугольникахI_AA'BиI_CC'Bравны острые углы при общей вершинеB, значит, равны и другие острые углы, то есть  ∠BI_AA'= ∠BI_CC'.  Поскольку углы, прилежащие к стороне треугольника I_AOI_C , равны, то этот треугольник равнобедренный. ЕслиOP– его высота, тоP– серединаI_AI_C.   Заметим, что точкиA', C'иPлежат на окружности с диаметромOB.  AI_A⊥AI_C  (и  СI_A⊥СI_C)  как биссектрисы смежных углов. Значит, точкиAиCлежат на окружности с диаметромI_AI_C, аP– центр этой окружности. Центральный уголCPI_Aэтой окружности вдвое больше вписанного углаCAI_A, равного половине углаA(так какAI_A– биссектриса этого угла). Значит, ∠CPI_A= ∠A.  Поскольку  ∠PBC= 180° – ∠CPI_A= 180° –A,  то четырёхугольникAPBC– вписанный, следовательно, точкаPлежит на описанной окружности треугольникаABCи, в то же время, – на описанной окружности треугольникаA'BC', то есть совпадает с точкойB₁.   Аналогично точкиA₁иC₁– середины сторон соответственноI_BI_CиI_AI_BтреугольникаI_AI_BI_C. Значит, стороны треугольникаA₁B₁C₁соответственно параллельны сторонам треугольникаI_AI_BI_C.   ПустьA'', B''иC''– точки касания вписанной окружности треугольникаABCсо сторонамиBC, ACиABсоответственно. Поскольку  B₁A'' = B₁C''  (как отрезки касательных, проведённых к окружности из одной точки), то треугольникB₁A''C''– равнобедренный. БиссектрисаB₁I_Aего внешнего угла при вершине параллельна основаниюA''C''. Следовательно,  A''C'' || I_AI_C.  Аналогично  A''B'' || I_AI_B  и  B''C'' || I_BI_C.   Ранее было доказано, что стороны треугольникаA₁B₁C₁соответственно параллельны сторонам треугольникаI_AI_BI_C. Значит, стороны треугольникаA₁B₁C₁соответственно параллельны сторонам треугольникаA''B''C''. Следовательно, треугольникI_AI_BI_Cподобен треугольникуA''B''C''.

Ответ задачи отсутствует