Олимпиадная задача по планиметрии: выпуклый пятиугольник с тупыми углами (Кноп К. А.)
Задача
Существует ли выпуклый пятиугольник (все углы меньше180o ) ABCDE , у которого все углы ABD , BCE , CDA , DEB и EAC – тупые?
Решение
Пусть, для определённости, AC – наименьшая диагональ пятиугольника.
Поскольку AC 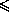 AD , то в треугольнике ACD угол DCA не
меньше угла ADC . Но тогда в этом треугольнике два тупых угла, что
невозможно.
AD , то в треугольнике ACD угол DCA не
меньше угла ADC . Но тогда в этом треугольнике два тупых угла, что
невозможно.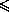
Ответ
Не существует.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет