Олимпиадная задача по планиметрии для 8–9 класса: окружность в треугольнике ABC

Решение 1:   Через вершину C проведём прямую, параллельную стороне AB. Пусть проведённая прямая пересекается с прямой B₁C₁ в точке D₁. Треугольник CD₁B₁ подобен равнобедренному треугольнику AC₁B₁. Значит,  CD₁ = CB₁.  Теперь достаточно доказать, что точка D совпадает с D₁, то есть что прямая A₁K проходит через точку D₁.

  Поскольку  CD₁ = CB₁ = CA₁,  то треугольник CA₁D₁ – равнобедренный. Поэтому  ∠CA₁D₁ = ½ (180° – ∠A₁CD₁) = ½ ∠B.

  Пусть I – центр вписанной окружности треугольника ABC. Тогда  ∠CBI = ½ ∠B = ∠CA₁D₁.  Значит,  A₁D₁ || BI.

  С другой стороны,  BI ⊥ A₁C₁,  а так как  A₁K ⊥ A₁C₁  (C₁K – диаметр окружности), то  A₁K || BI.  Значит, точки A₁, K и D₁ лежат на одной прямой.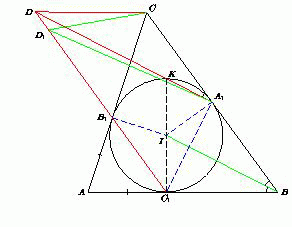

Решение 2:   Обозначим  ∠C = γ.  Тогда  ∠A₁IB₁ = 180° – γ,  ∠A₁ C₁B₁ = ½ ∠A₁IB₁ = 90° – ^γ/₂.

  Из прямоугольного треугольника DA₁C₁ находим, что  ∠A₁DC₁ = 90° – A₁C₁D = ^γ/₂ = ½ A₁CB₁.  При этом  CA₁ = CB₁,  значит, точки A₁, B₁ и D лежат на окружности с центром C. Следовательно,  CD = CB₁.

Ответ задачи отсутствует