Назад

Олимпиадная задача по планиметрии для 8–9 класса: координаты середины отрезка

Задача 208531 • Сложность: 2 • 8-9 класс
Задача

Пусть  M(x0, y0)  – середина отрезка с концами в точках  A(x1, y1)  и  B(x2, y2).  Докажите, что  x0 = ½ (x1 + x2),  y0 = ½ (y1 + y2).

Разделы:
Планиметрия Геометрические методы
Источники:
Система задач по геометрии Р.К.Гордина (zadachi.mccme.ru) Интернет-ресурсы
Количество версий:
5
Решение

  Пусть различные точки  Ax(x1, 0)  и  Bx(x2, 0)  расположены на оси OX, а Mx(x0, ;0)  – середина отрезка AxBx. Поскольку  AxMx = BxMx,  то

|x0 – x1| = |x0 – x2|.  Значит, либо  x0 – x1 = x0 – x2  (что невозможно, так как  x1 ≠ x2),  либо  x1 – x0 = x0 – x2,  откуда находим, что  x0 = ½ (x1 + x2).  Аналогично для точек, расположенных на оси OY.

  Если  M(x0, y0) – середина отрезка с концами в точках  A(x1, y1)  и  B(x2, y2)  и при этом  x1 ≠ x2  и  y1 ≠ y2,  то проекции Mx и My точки M на оси OX и OY – середины отрезков AxBx и AyBy. Поэтому  x0 = ½ (x1 + x2),  y0 = ½ (y1 + y2).

  Если  x1 = x2,  то точки Ax и Bx совпадают, поэтому   x0 = x1 = x2.  Значит, формула верна и в этом случае. Аналогично для   y1 = y2.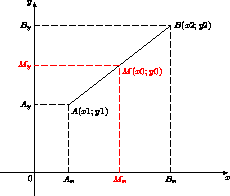

Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет