Олимпиадная задача по планиметрии для 8-9 классов от Гальперина В.
Задача
Около остроугольного треугольника ABC описана окружность с центром O. Перпендикуляры, опущенные из точки O на стороны треугольника, продолжены до пересечения с окружностью в точках K, M и P. Докажите, что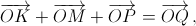 
где Q – центр вписанной окружности треугольника ABC.
Решение
Ясно, что K, M и P – середины дуг BC, AC и AB (пусть в таком порядке). BM и CP – биссектрисы углов B и C. Пусть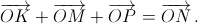 
Все слагаемые равны по модулю, поэтому вектор 
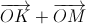направлен по биссектрисе угла KOM, которая параллельна биссектрисе CP (прямые OK и OM перпендикулярны сторонам угла C). Значит, вектор 
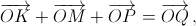лежит на прямой PC, то есть точка N лежит на биссектрисе CP. Аналогично доказывается, что точка N лежит и на биссектрисе BM, то есть совпадает с точкой Q пересечения биссектрис.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь