Олимпиадная задача по планиметрии: биссектрисы в четырёхугольнике, 8-9 класс

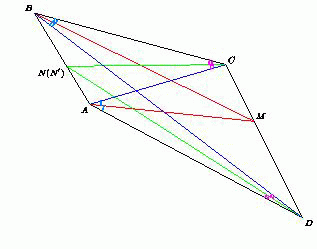
Пусть биссектрисы углов CAD и CBD пересекаются в точке M, лежащей на стороне CD. Биссектриса треугольника делит его сторону на отрезки, пропорциональные двум другим сторонам, поэтому  AD : AC = DM : MC = BD : BC.  Значит,  AD : BD = AC : BC.  Если биссектрисы углов ADB и ACB пересекают сторону AB в точках N и N' соответственно, то  AN : BN = AD : BD = AC : BC = AN' : BN'.  Следовательно, точки N и N' совпадают.

Ответ задачи отсутствует