Олимпиадная задача по планиметрии: Ортоцентр и описанная окружность треугольника

Пусть H – ортоцентр треугольника ABC , L – середина стороны AC , O – центр описанной окружности, H' – точка пересечения прямых BO и HL .

Поскольку расстояние от ортоцентра треугольника до его вершины вдвое больше расстояния от центра описанной окружности до стороны, противоположной этой вершине, OL = 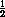BH , а т.к. OL || BH , то OL – средняя линия треугольника BHL' . Значит, O – середина отрезка BL' . Следовательно, BL' – диаметр окружности, т.е. точка L' лежит на описанной окружности треугольника ABC .

Ответ задачи отсутствует