Олимпиадная задача: угол между прямыми CK и BD в прямоугольнике ABCD, 8-9 класс
Задача
В прямоугольнике ABCD даны стороны AB = 3, BC = 4. Точка K удалена от точек A , B и C на расстояния 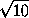 , 2 и 3
соответственно. Найдите угол между прямыми CK и BD .
, 2 и 3
соответственно. Найдите угол между прямыми CK и BD .
Решение
В плоскости ABCD рассмотрим прямоугольник BCPQ , симметричный данному прямоугольнику ABCD относительно прямой BC . Обозначим KQ = x . Отрезок KB – медиана треугольника AKQ . По формуле для медианы
KB2 = 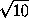 (2KA2 + 2KQ2 - AQ2),
(2KA2 + 2KQ2 - AQ2),
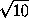 (2· 10 + 2· x2 - 36),
(2· 10 + 2· x2 - 36),
В треугольнике KQC известно, что
CQ = BD = 5, KC = 3, KQ = 4.
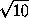 CKQ = 90o, sin
CKQ = 90o, sin 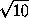 KCQ =
KCQ = 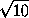 =
= 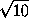 .
.
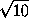 .
.
Ответ
arcsin 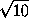 .
.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет