Олимпиадная задача по планиметрии и стереометрии: найти угол между прямыми AC и BD
Задача
Найдите угол между прямыми AC и BD , если AC = 6, BD = 10, а расстояние между серединами AD и BC равно 7.
Решение
Пусть M , N , K и L – середины отрезков AD , BC , AB и CD соответственно. Так как ML и KN – средние линии треугольников ADC и ABC с общим основанием AC , то ML || KN и
ML = KN = 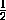 AC = 3.
AC = 3.
MK = LN = 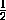 BD = 5.
BD = 5.
cos  MLN =
MLN = 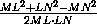 =
=
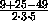 = -
= -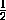 .
.
 MLN = 120o . Угол между прямыми AC и BD равен углу
между параллельными им прямыми LM и LN , т.е.60o .
MLN = 120o . Угол между прямыми AC и BD равен углу
между параллельными им прямыми LM и LN , т.е.60o .
Ответ
60o .
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет