Олимпиадная задача по стереометрии для 8–9 классов: расстояние от точки до плоскости
Задача
Точки A и B лежат в плоскости α , M – такая точка в пространстве, для которой AM = 2, BM = 5и ортогональная проекция на плоскость α отрезка BM в три раза больше ортогональной проекции на эту плоскость отрезка AM . Найдите расстояние от точки M до плоскости α .
Решение
Пусть M1– основание перпендикуляра, опущенного из точки M на плоскость α . Тогда AM1и BM1– ортогональные проекции отрезков соответственно AM и BM на эту плоскость, длина отрезка MM1– расстояние от точки M до плоскости α , а треугольники AMM1и BMM1– прямоугольные. Обозначим AM1 = x . Тогда по условию задачи BM1 = 3x . По теореме Пифагора
AM2 - AM21 = BM2 - BM21, или4 - x2 = 25 - 9x2,
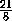 . Следовательно,
. Следовательно,
MM1 = 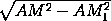 =
= 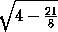 =
= 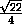 .
.
Ответ
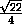 .
.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет