Олимпиадная задача: Свойства магического квадрата 3×3 — доказательство формул (Грибалко А. В.)
Задача
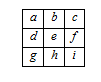 В квадрате 3×3 расставлены числа (см. рис.). Известно, что
квадрат магический: сумма чисел в каждом столбце, в каждой строке и на каждой
диагонали одна и та же. Докажите, что
В квадрате 3×3 расставлены числа (см. рис.). Известно, что
квадрат магический: сумма чисел в каждом столбце, в каждой строке и на каждой
диагонали одна и та же. Докажите, что
а) 2(a + c + g + i) = b + d + f + h + 4e.
б) 2(a³ + c³ + g³ + i³) = b³ + d³ + f ³ + h³ + 4e³.
Решение
Решение 1: а) Прибавив к обеим частям b + d + f + h, получим очевидное равенство
2) Докажем сначала равенство 2(a² + c² + g² + i²) = b² + d² + f² + h² + 4e². Для этого запишем его в виде
Решение 2: Сложив четыре суммы: по средней строке, среднему столбцу и диагоналям, мы получим сумму всех чисел таблицы плюс утроенное число в центральной клетке: 4S = 3S + 3e, то есть S = 3e.
Поскольку a + i = c + g = S – e = 2e, обозначим a = e + u, i = e – u, c = e + v, g = e – v.
Последовательно находим b = S – (a + c) = e – u – v, h = S – (g + i) = e + u + v, d = S – (a + g) = e – u + v, f = e + u – v.
Теперь равенство из п. а) очевидно. Для проверки равенства п. б) мы будем многократно использовать очевидное соотношение
(x + y)³ + (x – y)³ = 2x³ + 6xy². Имеем:
2(a³ + c³ + g³ + i³) = 2((e + u)³ + (e – u)³ + (e + v)³ + (e – v)³) = 8e³ + 12e(u² + v²),
b³ + d³ + f³ + h³ + 4e³ = (e – u – v)³ + (e + v – u)³ + (e + u – v)³ + (e + u + v)³ + 4e³ = 2e³ + 6e(u + v)² + 2e³ + 6e(u – v)² + 4e³ = 8e³ + 12e(u² + v²).
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь