Задание олимпиады: обёртки картины 1×1 — комбинаторная геометрия, 8

Задача

Обёрткой плоской картины размером 1×1 назовём прямоугольный лист бумаги площади 2, которым можно, не разрезая его, полностью обернуть картину с обеих сторон. Например, прямоугольник 2×1 и квадрат со стороной 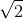– обёртки.

а) Докажите, что есть и другие обёртки. б) Докажите, что обёрток бесконечно много.

Решение

а) Процесс обёртывания прямоугольником 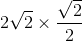изображён на рисунке.

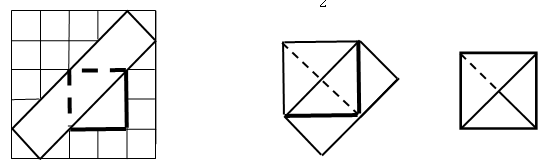
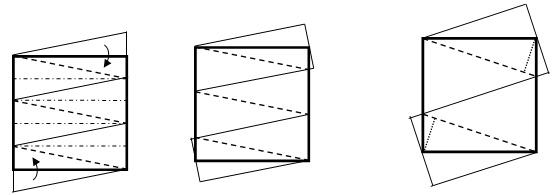
б) Разделим вертикальные стороны квадрата на n частей. На рис. слева показана обёртка квадрата параллелограммом, меньшая сторона которого равна ²/_n (изображён случай n = 5). На рис. в центре показано, как превратить параллелограмм в прямоугольник (при этом выступаюшие за горизонтальные стороны квадрата прямоугольные треугольники распадаются на две части). На рис. справа показано (для n = 3) как их надо загибать.

Ответ

Ответ задачи отсутствует

Олимпиадная задача: Обёртки для картины 1×1 — комбинаторная геометрия для 8–10 классов

Задача

Решение

Ответ

Подтверждение удаления