Олимпиадная задача по планиметрии для 9–11 классов от Филимонова В.П.
Задача
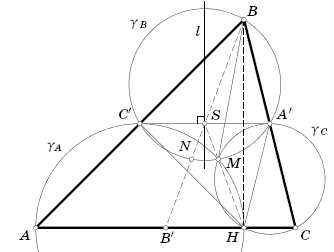
Точки A' , B' и C' "– середины сторон BC , CA и AB треугольника ABC соответственно, а BH "– его
высота. Докажите, что если описанные около треугольников AHC' и CHA' окружности проходят через точку M , отличную от H , то  ABM=
ABM= CBB' .
CBB' .
Решение
Пусть A и C – окружности, описанные около треугольников AHC' и CHA' соответственно. Так как точки B и H симметричны относительно средней линии A'C' треугольника ABC , то C'H=C'B=C'A ; A'H=A'B=A'C , т.е. треугольники AHC' и CHA' равнобедренные. Поэтому A'C' ( || AC ) – общая касательная к окружностям A и C .
 CBB'=
CBB'= CBS .
Пусть B – окружность, описанная вокруг треугольника BA'C' . Покажем, что точка M лежит на этой
окружности. Действительно, если α , β , γ –
углы треугольника ABC , то
CBS .
Пусть B – окружность, описанная вокруг треугольника BA'C' . Покажем, что точка M лежит на этой
окружности. Действительно, если α , β , γ –
углы треугольника ABC , то  C'MA'=
2π -
C'MA'=
2π - C'MH-
C'MH- A'MH=2π-(π-α)-(π-γ)= α+γ=
π-β .
A'MH=2π-(π-α)-(π-γ)= α+γ=
π-β .
 HSC'=
HSC'=
 BSC'=
BSC'=  A'SB' , отрезки SH и SB' симметричны
относительно l . Значит, точка N , симметричная точке M относительно l , лежит на B и на BB' , а дуги C'M и NA' равны. Вписанные углы
A'SB' , отрезки SH и SB' симметричны
относительно l . Значит, точка N , симметричная точке M относительно l , лежит на B и на BB' , а дуги C'M и NA' равны. Вписанные углы  C'BM и
C'BM и  A'BN опираются на эти дуги, т.е. равны. Итак,
A'BN опираются на эти дуги, т.е. равны. Итак,  ABM=
ABM=  C'BM=
C'BM=  A'BN=
A'BN=  CBB' .
CBB' .
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет