Олимпиадная задача по планиметрии и комбинаторной геометрии для 9-11 классов: точки в разбитом правильном треугольнике
Задача
Докажите, что существует такое натуральное число n , что если правильный треугольник со стороной n разбить прямыми, параллельными его сторонам, на n2 правильных треугольников со стороной 1, то среди вершин этих треугольников можно выбрать1993n точек, никакие три из которых не являются вершинами правильного треугольника (не обязательно со сторонами, параллельными сторонам исходного треугольника).
Решение
Пусть для некоторого n указанное в задаче разбиение произведено. Раскрасим вершины треугольников в 3 цвета, как на 114, где цвета обозначены буквами A , B , C . Заметим, что у любого правильного треугольника с вершинами в этих точках все вершины либо разноцветные, либо одноцветные. Убедиться в этом можно, проверив, что если такой треугольник повернуть вокруг любой его вершины (без потери общности можно считать, что она имеет цвет A ) на угол60o , то вершины, оставшиеся после поворота в исходном треугольнике и имевшие цвет A , сохранят его, а имевшие цвет B и C – поменяют его на C и B соответственно (если одна из вершин правильного треугольника с вершинами в покрашенных точках совпадает с центром поворота, то одна из оставшихся вершин переходит в другую).
Выберем цвет, которым покрашено наименьшее число точек, и выбросим точки этого цвета. Эту операцию
назовем разрежением. Останется не менее 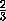 ·
· 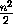 точек двух цветов
(так как точек было больше, чем
точек двух цветов
(так как точек было больше, чем 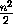 ).
Любой правильный треугольник с вершинами в этих точках одноцветный, а значит, имеет сторону
длиной не менее
).
Любой правильный треугольник с вершинами в этих точках одноцветный, а значит, имеет сторону
длиной не менее 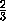 .
.
Рассмотрим отдельно множество точек каждого из двух оставшихся цветов, которые образуют часть
треугольной решетки со стороной 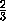 , и сделаем аналогичное разрежение. В результате останется
не менее(
, и сделаем аналогичное разрежение. В результате останется
не менее(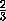 )2·
)2· 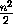 точек, которые могут образовывать вершины
правильного треугольника только со стороной не менее(
точек, которые могут образовывать вершины
правильного треугольника только со стороной не менее(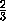 )2 . Действуя аналогично, после k -го разрежения, мы сохраним не менее(
)2 . Действуя аналогично, после k -го разрежения, мы сохраним не менее(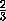 )k·
)k· 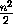 точек, а
правильные треугольники будут иметь сторону не менее. чем(
точек, а
правильные треугольники будут иметь сторону не менее. чем(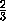 )k .
)k .
Пусть n=3m , тогда после k=2m+1разрежений, правильных треугольников не останется вовсе, а
точек останется не менее, чем(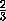 )2m+1·
)2m+1· 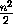 =(
=(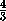 )m·
)m· 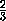
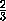 1993· n ,
при(
1993· n ,
при(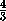 )m
)m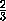 3· 1993.
Таким образом, достаточно взять m>log
3· 1993.
Таким образом, достаточно взять m>log 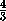 ((3· 1993)).
((3· 1993)).
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь