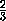
Пусть даны прямоугольные параллелепипеды
ABCDA'B'C'D' и
A1B1C1D1A'1B'1C'1D'1 равного
объема, который мы будем считать единичным.
Обозначим длины их ребер через
a ,
b ,
c и
a1 ,
b1 ,
c1 соответственно.
Если у параллелепипедов есть равные ребра, например
a=a1 , то
достаточно поставить параллелепипеды на горизонтальную плоскость так, чтобы ребра
a и
a1 были
перпендикулярны ей, так как тогда любое их сечение горизонтальной плоскостью будет иметь площадь
bc=b1c1 . Поэтому далее будем считать, что длины ребер параллелепипедов различны.
Всюду буквами
S и
V обозначим площадь и объем соответственно.
Мы покажем, что на ребрах
AA' и
A1A'1 параллелепипедов найдутся точки
M и
M1 такие, что
SMBD=SM1B1D1 и
VAMBD=VA1M1B1D1 . Далее мы получим, что расположение
параллелепипедов, при котором плоскости
MBD и
M1B1D1 горизонтальны
и совпадают (рис.), удовлетворяет условию.
Докажем предварительно несколько вспомогательных утверждений.
Лемма 1.Пусть в пирамиде
ABCD плоские углы при вершине
A прямые, а площади граней
BCD ,
ABC ,
ABD и
ACD равны
S0 ,
S1 ,
S2 и
S3 соответственно. Тогда
S02=S12+S22+S32 .
Спроектируем пирамиду ортогонально сначала на плоскость
ABC , затем на плоскости
ABD ,
ACD и
BCD (рис.). Обозначим углы, образуемые гранями
ABC ,
ABD и
ACD с гранью
BCD через
α1 ,
α2 и
α3 . Тогда по теореме о площади ортогональной проекции
многоугольника
Si=S0· cosαi (
i=1
,2
,3),
S0=S1 cosα1+S2 cosα2+S3 cosα3 , поэтому
cos2α1+ cos2α2+ cos2α3=1и
S02=S12+S22+S32 . Лемма 1 доказана.
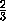
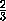
Рассмотрим четырехугольную пирамиду
EABCD (
ABCD – прямоугольник), лежащую на горизонтальной
плоскости гранью
EAB (рис.). Такую пирамиду назовем клином с основанием
EAB , а
расстояние от прямой
CD до плоскости
EAB назовем высотой клина. Пусть площадь основания клина
EABCD равна, а его высота равна
H .
Лемма 2.Объем клина равен двум третям произведения площади его основания на высоту, т.е.
V=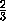 · H
· H .
Разобьем клин на две пирамиды
DEAB и
DEBC . Их объемы равны, так как
SABD=SBCD и
расстояние от точки
E до их оснований одно и то же. Поэтому
V=2
VDEAB=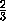 H
H .
Лемма 3.На горизонтальной плоскости стоят два тетраэдра(или два клина)с равными высотами и равными
площадями оснований. Тогда их сечения плоскостью, параллельной основаниям, имеют равные площади.
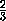
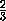
В случае тетраэдров (рис) из подобия получаем, что
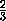 =
=(
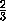
)
2 и
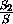 =
=(
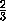
)
2 , следовательно,
S1=S2 . Чтобы доказать это
утверждение для клиньев, достаточно достроить клин до призмы (рис.).
Из рисунка видно, что
x= -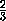 =
= (1
-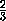
),
откуда и следует равенство площадей сечений.
Докажем теперь существование точек
M и
M1 . Если
AM=xc , а
A1M1=xc1 , где
x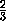
(0
,1], то равенство объемов пирамид
AMBD и
A1M1B1D1 выполняется автоматически, а
равенство площадей треугольников
MBD и
M1B1D1 равносильно равенству
f(
x)
=(
a2c2+b2c2-a11c12-b12c12)
x2+(
a2b2-a12b12)
=0, так как
SMBD2=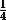
(
x2a2c2+x2b2c2+a2b2)и
SM1B1D12=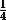
(
x2a12c12+x2b12c12+a12b12)в силу леммы 1.
Покажем, что
f(0)
>0, а
f(1)

0(или наоборот). Отсюда и будет
следовать существование
x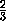
(0
,1]такого, что
f(
x)
=0, а, значит, и
существование точек
M и
M1 .
Заметим, что
f(0)
=a2b2-a12b12= -
-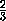 =
=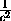 -
-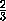
и, аналогично,
f(1)
=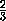 +
+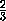 +
+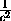 -
-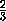 -
-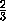 -
-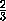
, так
как
abc=a1b1c1=1.
Рассмотрим два новых прямоугольных параллелепипеда: один с ребрами
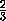
,
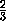
,
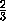
и диагональю
d , другой – с ребрами
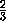
,
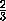
,

и диагональю
d1 : их объемы равны единице, а диагональ одного из них не
меньше, чем диагональ другого. Пусть, скажем,
d d1
d1 , тогда
f(1)

0. Так как объемы параллелепипедов равны, то у первого
параллелепипеда найдется ребро, большее какого-нибудь ребра второго (выше мы предполагали, что равных ребер
нет). Изменив в случае необходимости обозначения, будем считать, что
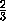 >
>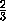
.
Тогда
f(0)
>0, что и требовалось.
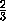
Осталось доказать, что описанное выше расположение параллелепипедов удовлетворяет условию. Ясно,
что в силу симметрии параллелепипедов относительно своих центров, достаточно проверить это
утверждение для их половинок, т.е. призм
ABDA'B'D' и
A1B1D1A'1B'1D'1 . Для пирамид
MABD и
M1A1B1D1 справедливость его следует из леммы3.
Проведем плоскость
A'FE|| MBD (рис) и плоскость
A'1F1E1|| M1B1D1 .
Эти плоскости отсекают от призм клинья
A'B'D'FE и
A'1B'1D'1F1E1 равного объема, так как
(в силу леммы 2)
VA'B'D'FE=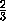 ·
· 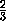 axc· b=
axc· b=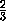 x=
x=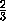 ·
· 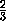 a1xc1· b1=
VA'1B'1D'1F1E1.
a1xc1· b1=
VA'1B'1D'1F1E1.
Так как площади оснований и объемы клиньев равны, то равны и их высоты, поэтому в силу леммы 3
утверждение справедливо и для клиньев.
Остается заметить. что призмы
MBDA'EF и
M1B1D1A'1E1F1 имеют равные площади оснований и
равные объемы (а, следовательно, и равные высоты), поэтому площади их сечений любой горизонтальной
плоскостью равны.
Аналогичное утверждение для произвольных фигур равного объема, вообще говоря, неверно
(см. также задачу 10.6 и замечания к ней).
В условии задачи можно отказаться от прямоугольности
параллелепипедов. Утверждение при этом остается справедливым. Кроме того,
оно справедливо для произвольных равновеликих тетраэдров, однако известное
доказательство этого факта неэлементарно.
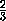
 · H .
Разобьем клин на две пирамиды DEAB и DEBC . Их объемы равны, так как SABD=SBCD и
расстояние от точки E до их оснований одно и то же. Поэтому V=2VDEAB=
· H .
Разобьем клин на две пирамиды DEAB и DEBC . Их объемы равны, так как SABD=SBCD и
расстояние от точки E до их оснований одно и то же. Поэтому V=2VDEAB=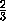 H .
Лемма 3.На горизонтальной плоскости стоят два тетраэдра(или два клина)с равными высотами и равными
площадями оснований. Тогда их сечения плоскостью, параллельной основаниям, имеют равные площади.
H .
Лемма 3.На горизонтальной плоскости стоят два тетраэдра(или два клина)с равными высотами и равными
площадями оснований. Тогда их сечения плоскостью, параллельной основаниям, имеют равные площади.
 =(
=(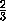 )2 и
)2 и 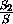 =(
=(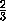 )2 , следовательно, S1=S2 . Чтобы доказать это
утверждение для клиньев, достаточно достроить клин до призмы (рис.).
Из рисунка видно, что x= -
)2 , следовательно, S1=S2 . Чтобы доказать это
утверждение для клиньев, достаточно достроить клин до призмы (рис.).
Из рисунка видно, что x= -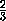 = (1-
= (1-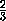 ),
откуда и следует равенство площадей сечений.
Докажем теперь существование точек M и M1 . Если AM=xc , а A1M1=xc1 , где x
),
откуда и следует равенство площадей сечений.
Докажем теперь существование точек M и M1 . Если AM=xc , а A1M1=xc1 , где x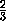 (0,1], то равенство объемов пирамид AMBD и A1M1B1D1 выполняется автоматически, а
равенство площадей треугольников MBD и M1B1D1 равносильно равенству f(x)=(a2c2+b2c2-a11c12-b12c12)x2+(a2b2-a12b12)=0, так как SMBD2=
(0,1], то равенство объемов пирамид AMBD и A1M1B1D1 выполняется автоматически, а
равенство площадей треугольников MBD и M1B1D1 равносильно равенству f(x)=(a2c2+b2c2-a11c12-b12c12)x2+(a2b2-a12b12)=0, так как SMBD2=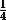 (x2a2c2+x2b2c2+a2b2)и SM1B1D12=
(x2a2c2+x2b2c2+a2b2)и SM1B1D12=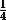 (x2a12c12+x2b12c12+a12b12)в силу леммы 1.
Покажем, что f(0)>0, а f(1)
(x2a12c12+x2b12c12+a12b12)в силу леммы 1.
Покажем, что f(0)>0, а f(1) 0(или наоборот). Отсюда и будет
следовать существование x
0(или наоборот). Отсюда и будет
следовать существование x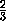 (0,1]такого, что f(x)=0, а, значит, и
существование точек M и M1 .
Заметим, что f(0)=a2b2-a12b12=
(0,1]такого, что f(x)=0, а, значит, и
существование точек M и M1 .
Заметим, что f(0)=a2b2-a12b12= -
-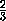 =
=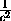 -
-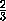 и, аналогично, f(1)=
и, аналогично, f(1)=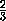 +
+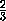 +
+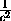 -
-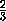 -
-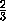 -
-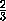 , так
как abc=a1b1c1=1.
Рассмотрим два новых прямоугольных параллелепипеда: один с ребрами
, так
как abc=a1b1c1=1.
Рассмотрим два новых прямоугольных параллелепипеда: один с ребрами 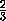 ,
, 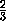 ,
, 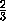 и диагональю d , другой – с ребрами
и диагональю d , другой – с ребрами 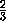 ,
, 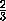 ,
,  и диагональю d1 : их объемы равны единице, а диагональ одного из них не
меньше, чем диагональ другого. Пусть, скажем, d
и диагональю d1 : их объемы равны единице, а диагональ одного из них не
меньше, чем диагональ другого. Пусть, скажем, d d1 , тогда f(1)
d1 , тогда f(1) 0. Так как объемы параллелепипедов равны, то у первого
параллелепипеда найдется ребро, большее какого-нибудь ребра второго (выше мы предполагали, что равных ребер
нет). Изменив в случае необходимости обозначения, будем считать, что
0. Так как объемы параллелепипедов равны, то у первого
параллелепипеда найдется ребро, большее какого-нибудь ребра второго (выше мы предполагали, что равных ребер
нет). Изменив в случае необходимости обозначения, будем считать, что 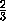 >
>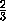 .
Тогда f(0)>0, что и требовалось.
.
Тогда f(0)>0, что и требовалось.
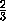
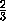 ·
· 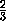 axc· b=
axc· b=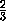 x=
x=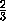 ·
· 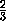 a1xc1· b1=
VA'1B'1D'1F1E1.
a1xc1· b1=
VA'1B'1D'1F1E1.