Олимпиадная задача по планиметрии: прямоугольники равной площади (8-10 класс)
Задача
Верно ли, что любые два прямоугольника равной площади можно расположить на плоскости так, что любая горизонтальная прямая, пересекающая один из них, будет пересекать и второй, причём по отрезку той же длины?
Решение
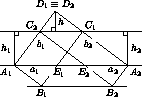
Пусть даны два прямоугольника равной площади: A1B1C1D1 со сторонами a1 и b1 и A2B2C2D2 со сторонами a2 и b2. Без ограничения общности будем считать, что a1 < b2 и a2 < b1 (если a1 = b2, то в силу равенства площадей и a2 = b1, в этом случае утверждение очевидно). Расположим прямоугольники так, как показано на рисунке, и докажем, что это расположение удовлетворяет условию задачи.
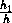 =
= 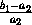 и
и 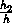 =
= 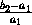 . Так как a1b1 = a2b2, то
. Так как a1b1 = a2b2, то
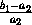 =
= 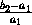 , следовательно, h1 = h2 и A1A2 || C1C2. Из этого вытекает, что четырёхугольники A1E1C1C2 и A2E2C2C1 – параллелограммы (значит,
, следовательно, h1 = h2 и A1A2 || C1C2. Из этого вытекает, что четырёхугольники A1E1C1C2 и A2E2C2C1 – параллелограммы (значит,
A1E1 = A2E2), и площади их равны. Тогда, в силу равенства площадей прямоугольников, равны и площади треугольников A1B1E1 и A2B2E2, а так как
A1E1 = A2E2, то равны их высоты. Поэтому B1B2 || A1A2. Следовательно, Следовательно, A1E2B2B1 – параллелограмм, и треугольники A1B1E1 и E2B2A2 равны по катету и гипотенузе. Из этого следует, что любая горизонтальная прямая, пересекающая эти треугольники, пересекает их по равным отрезкам. Если же горизонтальная прямая пересекает параллелограммы A1E1C1C2 и A2E2C2C1 или совпадающие треугольники C1D2C2 и C1D1C2, то равенство соответствующих отрезков очевидно.
Ответ
Верно.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь