Олимпиадная задача по планиметрии для 8—11 классов с окружностями и точкой F
Задача
Две окружностиS1иS2касаются внешним образом в точкеF. Их общая касательная касаетсяS1иS2в точкахAиBсоответственно. Прямая, параллельнаяAB, касается окружностиS2в точкеCи пересекает окружностьS1в точкахDиE. Докажите, что общая хорда описанных окружностей треугольниковABCиBDE, проходит через точкуF.
Решение
Точки A, F и C лежат на одной прямой (см. задачу 209566). Докажем, что центры описанных окружностей ω1 и ω2 треугольников ABC и BDE соответственно, лежат на AC. Поскольку общая хорда двух окружностей перпендикулярна линии центров и BF ⊥ FC (BC – диаметр S2), отсюда следует утверждение задачи.
Центр ω1 лежит на AC, так как треугольник ABC – прямоугольный.
Пусть радиусы S1 и S2 равны R и r соответственно. Тогда из прямоугольной трапеции BAO1O2, где O1 и O2 – центры S1 и S2,
находим AB = 2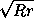 (рис. слева).
(рис. слева).
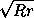
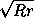
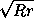 . Таким образом, AB = AD = AE, то есть центр окружности ω2совпадает сA.
. Таким образом, AB = AD = AE, то есть центр окружности ω2совпадает сA.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь