Олимпиадная задача Карпова: последовательности и геометрия для 8–10 классов
Задача
Натуральные числа от 1 до 1000 по одному выписали на карточки, а затем накрыли этими карточками какие-то 1000 клеток прямоугольника1x 1994. Если соседняя справа от карточки с числом n клетка свободна, то за один ход ее разрешается накрыть карточкой с числом n+1. Докажите, что нельзя сделать более полумиллиона таких ходов.
Решение
Заметим, что карточку с числом 1 двигать нельзя.
Следовательно, карточку с числом 2 можно двигать не более одного раза,
карточку с числом 3 – не более двух раз, и т.д.
Итак, для любого n
1000карточку с числом n можно двигать не более n-1раз
(так как мы можем положить ее только справа от карточки с числом n-1, которая, в свою очередь,
может двигаться не более n-2раз). Значит, число сделанных ходов не превосходит1+2+...+999=999·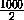 
=499,500<500,000.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь