Олимпиадная задача по математике: делимость в разрезанном прямоугольнике (классы 7–9)

  Ясно, что если прямоугольник m×n разрезан на уголки, то mn делится на 3. Пусть n кратно 3. Расставим в клетках прямоугольника числа так, как показано в таблице:

  Сумма всех этих чисел равна делится на 3. Сумма чисел, стоящих в уголке видаa, даёт при делении на 3 остаток 2; сумма чисел, стоящих в уголке видаb– остаток 1; суммы чисел, стоящих в уголках видаcиd, делятся на 3. Еслиn_aиn_b– количества уголков видаaи видаbсоответственно, то сумма всех чисел в прямоугольнике имеет вид  3N+ 2n_a + n_b= 3(N + n_b) + 2(n_a – n_b),  гдеN– некоторое целое число. Поэтому  2(n_a – n_b)  и, следовательно,  n_a – n_b  делится на 3.

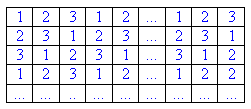
Ответ задачи отсутствует