Могут ли числа от 1 до 100 входить в 12 геометрических прогрессий? Олимпиадная задача для 9-11 классов

  Покажем, что три различных простых числа не могут входить в одну геометрическую прогрессию. Предположим противное:  p₁ < p₂ < p₃  – простые числа,   p₁ = aq^k,  p₂ = aq^m,  p₃ = aqⁿ.  Тогда  p₂ = p₁q^m-k = q^s,  p₃ = p₂q^n–m = q^r.  Отсюда 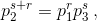   что невозможно, так как r и s – натуральные числа.

  Но среди чисел от 1 до 100 содержится 25 простых чисел, а в одну прогрессию могут входить не более двух из них.

Не могут.