Олимпиадная задача по стереометрии для 10-11 класса о высотах тетраэдра
Задача
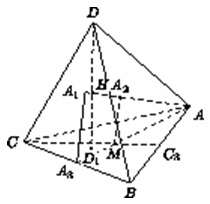
Высоты тетраэдра пересекаются в одной точке.
Докажите, что эта точка, основание одной из высот и три точки, делящие другие высоты в отношении 2 : 1, считая от вершин, лежат на одной сфере.
Решение
Пусть AA1, BB1, CC1, DD1 – высоты тетраэдра ABCD, H – точка их пересечения, A2, B2, C2 – точки, делящие высоты в отношении 2 : 1, считая от соответствующих вершин, M – точка пересечения медиан AA3, BB3, CC3 треугольника ABC. Докажем, что точки M, A2, B2, C2, D1 и H лежат на сфере с диаметром MH. Из подобия треугольников MAA2 и A3AA1 (AM : AA3 = AA2 : AA1 = 2 : 3) следует, что MA2 || A3A1, то есть MA2 ⊥ AA1, так как AA1 – высота тетраэдра и, значит, AA1 ⊥ A3A1. Аналогично MB2 ⊥ BB1 и MC2 ⊥ CC1. Наконец, DD1 – высота тетраэдра, поэтому MD1 ⊥ DD1.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь