Олимпиадная задача по планиметрии и стереометрии: сечение пирамиды и правильный многоугольник

  Пусть правильный (n+1)-угольник B₁...B_n+1 является сечением пирамиды SA₁...A_n, где A₁...A_n – правильный n-угольник. Мы рассмотрим три случая: n = 5,  n = 2k – 1  (k > 3)  и  n = 2k  (k > 2).

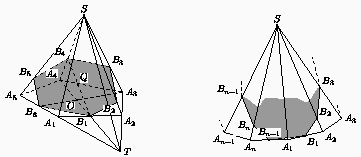
  Так как n-угольная пирамида имеет  n + 1  грань, то стороны сечения находятся по одной в каждой грани пирамиды. Поэтому без ограничения общности можно считать, что точки B₁, ..., B_n+1 расположены на ребрах пирамиды так, как показано на рисунках (в соответствии с указанными случаями).

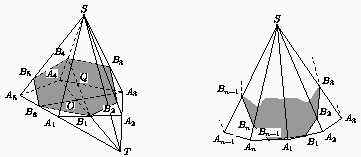
  1)  n= 5.  Так как в правильном шестиугольникеB₁...B₆прямыеB₂B₃,B₅B₆иB₁B₄параллельны, а плоскостиA₂SA₃иA₁SA₅проходят черезB₂B₃иB₅B₆, то их линия пересеченияST (T = A₁A₅A₂A₃)  параллельна этим прямым, то есть  ST || B₁B₄.   Проведём через прямыеSTиB₁B₄плоскость. Эта плоскость пересечет плоскость основания пирамиды по прямойB₁A₄, которая должна проходить через точку пересечения прямойSTс плоскостью основания, то есть через точкуT.   Итак, прямыеA₁A₅,A₄B₁иA₂A₃пересекаются в одной точке. Аналогично доказывается, что прямыеA₁A₂,A₃B₆иA₄A₅пересекаются в одной точке. Из этого следует, чтоA₄B₁иA₃B₆– оси симметрии правильного пятиугольникаA₁...A₅, значит, точкаOих пересечения – центр этого пятиугольника. Заметим теперь, что еслиQ– центр правильного шестиугольникаB₁...B₆, то плоскостиSA₃B₆,SA₄B₁иSB₂B₅пересекаются по прямойSQ. Следовательно, прямыеA₃B₆,A₄B₁иA₂A₅должны пересекаться в одной точке – точке пересечения прямойSQс плоскостью основания пирамиды. Значит, диагональ A₂A₅ правильного пятиугольникаA₁...A₅должна проходить через его центрO, что неверно.   2)  n = 2k – 1  (k > 3).  Аналогично первому случаю показывается, что так как в правильном 2k-угольнике B₁...B_2k прямые B₁B₂, B_k+1B_k+2 и B_kB_k+3 параллельны, то прямые A₁A₂, A_k+1A_k+2 и A_kA_k+3 должны пересекаться в одной точке или быть параллельными, что невозможно, так как в правильном (2k–1)-угольнике A₁...A_2k–1 прямые A_k+1A_k+2 и A_kA_k+3 параллельны, а прямые A₁A₂ и A_k+1A_k+2 не параллельны.   3)  n = 2k  (k > 2).  Аналогично предыдущему случаю прямые A₁A₂, A_k+1A_k+2 и A_kA_k+3 параллельны, следовательно, прямые B₁B₂, B_k+1B_k+2 и B_kB_k+3 должны пересекаться в одной точке, что невозможно, так как B_k+1B_k+2 || B_kB_k+3, а прямые B₁B₂ и B_k+1B_k+2 не параллельны.

Ответ задачи отсутствует