Олимпиадная задача по планиметрии и комбинаторной геометрии для 9–11 классов: сумма углов выпуклого многоугольника
Задача
Дан выпуклый многоугольник, никакие две стороны которого не параллельны. Для каждой из его сторон рассмотрим угол, под которым она видна из вершины, наиболее удалённой от прямой, содержащей эту сторону. Докажите, что сумма всех таких углов равна 180°.
Решение
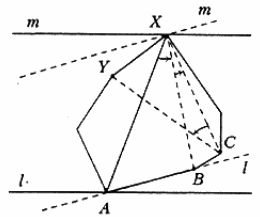
Можно считать, что среди сторон многоугольника нет горизонтальных. Проведём горизонтальные опорные прямые l и m этого многоугольника, то есть прямые, проходящие через некоторые его вершины (в данном случае это верхняя вершина X и нижняя – A), но не содержащие его внутренних точек. Назовём диагональ (или сторону) AX ведущим отрезком для опорных прямых l и m. Будем поворачивать прямые l и m против часовой стрелки так, чтобы они оставались параллельными и опорными, и следить за тем, как меняется ведущий отрезок. Впервые такое переключение произойдёт, когда одна из прямых l или m попадёт на сторону многоугольника.
На рис. l попадает на сторону AB, после чего ведущим станет отрезок XB. Заметим, что ведущий отрезок повернулся против часовой стрелки на угол AXB, под которым сторона AB видна из самой далекой от неё вершины X.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь