Олимпиадная задача по планиметрии: угол MKN прямой — интересно для 8–10 классов
Задача
Две окружности пересекаются в точках A и B. Через точку A проведена прямая, вторично пересекающая первую окружность в точке C, а вторую – в точке D. Пусть M и N – середины дуг BC и BD, не содержащих точку A, а K – середина отрезка CD. Докажите, что угол MKN прямой. (Можно считать, что точки C и D лежат по разные стороны от точки A.)
Решение
Решение 1: Пусть N1 – точка, симметричная точке N относительно K (см. рис.). Тогда треугольники KCN1 и KDN равны, поэтому
CN1 = ND и ∠N1CK = ∠NDK = 180° – ∠ABN.
Заметим еще, что ∠MCK = 180° – ∠ABM. Складывая полученные равенства, находим, что ∠N1CM = ∠MBN. Кроме того, из условия следует, что CM = MB и BN = ND (то есть и BN = CN1). Значит, треугольники MCN1 и MBN равны, откуда MN1 = MN. Отрезок MK – медиана равнобедренного треугольника MNN1, поэтому ∠MKN = 90°.
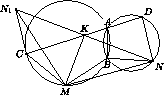
Решение 2: Рассмотрим композицию RM○RN поворота RN на угол α = ∠DNB и поворота RM на угол β = ∠BMC (углы предполагаются ориентированными). Заметим, что α + β = ±180°, поэтому ZX = RM○RN – центральная симметрия относительно некоторой точки X. Но ZX(D) = (RM○RN)(D) = RM(B) = C, поэтому X – середина отрезка CD, то есть совпадает с точкой K. Если N1 = ZK(N), то N1 = (RM○RN)(N) = RM(N), то есть треугольник NMN1 – равнобедренный и ∠MKN = 90°.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь