Олимпиадная задача: Может ли тетраэдр вместить сферу большего диаметра? Стереометрия, 10–11 класс
Задача
В тетраэдр ABCD , длины всех ребер которого не более 100, можно поместить две непересекающиеся сферы диаметра 1. Докажите, что в него можно поместить одну сферу диаметра 1,01.
Решение
Рассмотрим множества M центров сфер диаметра 1, лежащих в данном
тетраэдре T . Так как M – множество точек, удаленных от всех граней T не менее, чем на1/2, то M – это тетраэдр с гранями,
параллельными граням тетраэдра T , т.е. M и T гомотетичны.
Центры вписанных сфер обоих тетраэдров совпадают, поэтому коэффициент k гомотетии равен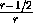 
, где r – радиус сферы,
вписанной в T .
С другой стороны, две сферы единичного диаметра не пересекаются, поэтому
расстояние между их центрами не меньше 1, значит, длина одного из ребер
тетраэдра M , содержащего эти центры, не меньше 1. Отсюда следует, что k
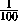(длины ребер тетраэдра T не больше 100), т.е.1-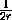
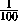, откуда2r
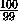>1,01.
Итак, диаметр сферы, вписанной в T , больше 1,01, т.е. в качестве
искомой можно выбрать сферу, вписанную в T .
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь