Олимпиадная задача по теории чисел на минимальное число, не представимое в виде суммы степеней для 8–10 классов
Задача
Найдите наименьшее натуральное число, не представимое в виде 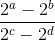 , где a, b, c, d – натуральные числа.
, где a, b, c, d – натуральные числа.
Решение
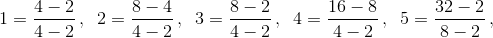
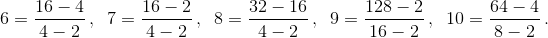 Предположим, что 11 =
Предположим, что 11 = 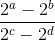 . . Не уменьшая общности, положим a > b, c > d. Обозначим m = a – b, n = c – d, k = b – d. Получаем
. . Не уменьшая общности, положим a > b, c > d. Обозначим m = a – b, n = c – d, k = b – d. Получаем
11(2n – 1) = 2k(2m – 1). Так как в левой части целое нечётное число, то k = 0. Заметим, что n = 1 не подходит. Если же m > n > 1, то 2m – 1 и 2n – 1 дают остаток 3 при делении на 4. Значит, левая и правая части дают соответственно остатки 1 и 3 при делении на 4. Противоречие.
Ответ
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет