Олимпиадная задача по планиметрии: окружности и деление периметра треугольника

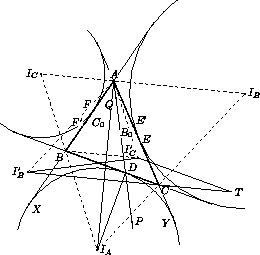
  Пусть B₀, C₀ – середины сторон AC, AB соответственно, σ_A – третья вневписанная окружность, P и Q – точки пересечения ω_B и ω_C. Положим  AB = c,

BC = a,  CA = b.  Обозначим через I_A, I_B, I_C, J_B, J_C центры окружностей σ_A, σ_B, σ_C, ω_B, ω_C соответственно; через D, E, F точки касания σ_A, σ_B, σ_C и сторон BC, CA, AB; через E', F' – точки касания ω_B, ω_C и сторон CA, AB; через X, Y – точки касания σ_A и продолжений сторон AB, BC соответственно (см. рис.).

  Известно, чтоADделит пополам периметр треугольникаABC(это следует из того, что  CD= ½ (a + c – b).  Поэтому достаточно показать, чтоAлежит наPQ, а  AD⊥J_BJ_C.   Ясно, чтоEиE'симметричны относительноB₀. Следовательно,  AE' = CE= ½ (b + c – a).  Аналогично  AF'= ½ (b + c – a).  Получаем, что касательные к ω_Bи ω_C, проведённые из точкиA, равны. ПоэтомуAлежит на радикальной осиPQокружностей ω_Bи ω_C.   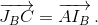Из симметрии следует, чтоAJ_BCI_B– параллелограмм, поэтому    Аналогично  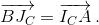  Построим такую точкуT, чтоBJ_CTC– параллелограмм.   Получаем: 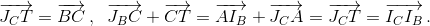   Так какAI_A  иI_BI_Cявляются внутренней и внешней биссектрисами углаBAC, тоAI_A⊥I_BI_C. Аналогично  BI_B⊥I_CI_A, CI_C⊥I_AI_B.  Следовательно,  I_AB = I_AI_Bcos∠I_BI_AI_C,  I_AC = I_AI_Ccos∠I_BI_AI_C.  Это означает, что треугольникиI_ABCиI_AI_BI_Cподобны. Заметим, чтоI_ADиI_AA– соответствующие высоты в подобных треугольникахI_ABCиI_AI_BI_C. Отсюда следует, что  I_AD:I_AA = BC:I_BI_C.   Рассмотрим треугольникиJ_BJ_CTиADI_A. Имеем:  J_BT || I_BI_C⊥I_AA, J_CT || BC⊥I_AD, J_CT:J_BT = BC:I_BI_C = I_AD:I_AA.  Отсюда следует, что треугольникиI_BI_CTиI_ADAподобны, и их соответствующие стороны перпендикулярны. Итак,  J_BJ_C⊥AD.

Ответ задачи отсутствует